Lab 03: Flow under a sluice gate - 120921 - 120927
[RDA] Good morning
...
[RDA] Today we are going to explain and demonstrate
the flow under a sluice gate using the energy principle.
...
...
[RDA] The theoretical formula based on the conservation of specific energy is:
...
...
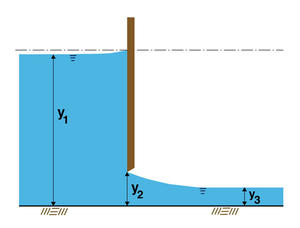
[RDA] in which Q is the discharge, B is the width of the flume, y1 is the upstream flow depth, y3 is the downstream flow depth, and g is the acceleration of gravity.
...
[RDA] This theoretical formula can be expressed in terms of the gate opening y2
by defining a contraction ratio Cc
...
...
[RDA] This leads to:
...
...
[RDA] in which the discharge coefficient Cd is:
...
...
...
[RDA] Now we turn on the pump on the demonstration flume.
...
[RDA]We set the bed slope equal to zero...
and check the level...
...
[Point to the width of the flume] [RDA] The width B of the flume is 6 inches, or 152.4 mm
...
[RDA] [Point to the point gage] Note that the point gage is at zero.
...
[RDA] Now we are going to measure the height to the bottom of the flume
...
[RDA] The height is X mm
...
[RDA] Now we are going to measure the height to the top of the gate opening
...
[RDA] The height is Y mm
...
[RDA] The gate opening y2 is equal to: ... X - Y
...
[RDA] Now we are going to measure the height to the water surface upstream of the sluice gate
...
...
[RDA] The height is Z mm
...
...
[RDA] The upstream head or depth y1 is equal to: ... X - Z
...
[RDA] Now we are going to measure the height to the water surface downstream of the sluice gate
...
[RDA] The height is V mm
...
...
[RDA] The downstream depth y3 is equal to: ... X - V
...
...
[RDA] Now we apply the theoretical formula in terms of upstream head y1 and downstream depth y3:
...
[RDA] The discharge is Q1 [actual number] liters per second.
...
[RDA] Next we apply the practical formula in terms of upstream head y1 and gate opening y2:
...
[RDA] The discharge is Q2 [actual number] liters per second.
...
[RDA] Note that both equations give the same answer: Q = ... .
...
[RDA] Thank you.
Q = B y1 y3 [ 2g / (y1 + y3) ]1/2
...
Cc = y3 / y2
Q = B Cd y2 (2g y1)1/2
Cd = Cc / [ 1 + Cc (y2 / y1)]1/2
